..this is a living document that I will update as I go....
...I do not guarantee it is finished now or ever will be...
...it is safe to assume I don't know what I'm talking about and am willing to learn...
..this is version 1.13; 2022-05-28
..previous versions 1.0-1.7; 2022-05-26; 1.8-1.12 2022-05-27
... I would like to give a special shout out to my colleague, Karina Gutierrez-Garcia, for helping me to get started with Robetta, AlphaFold, SAVES, and some other software, links, and advice I've still not had time to explore.
A little song and dance about the old days of protein structures:
I confess: I've been a warm body in the audience of many structural biology presentations, but my mind was elsewhere. I get it. I get it. That atom was a tricky one to place. That protein fold was unexpected, sure I guess. And that was something how the protein looked like a ball of yarn before you mutated the alanine at position 369, and still looked like a ball of yarn after.
There were some very good protein structure presentations I've been to as well. Usually about ribosomes. When a structural biologist is also a great presenter (rare in science generally), then it becomes fascinating. Look, it's just a little machine with gears, and ratcheting mechanisms, and scissors! This part here - look how it works like a socket wrench, and this part like a circuit switch. Look how this forms the hardest material in the biological world, and this other part that makes it flexible. See the lattice work!
I've always been glad there were structural biologists crystallizing proteins, doing NMR, cryo-EM, etc; but I was content to not do it myself. It is one of those branches of science that you understand is necessary and foundation-building; that has already yielded big rewards, and will continue to do so slowly but surely; but that seems somewhat sectioned off from what most researchers are doing. The average biologist may have thought, "Sure, it'd be amazing to have the structure to all my favorite proteins, whether to help with designing mutational strategies, to search for 'structural homology', or to just see the little nuts, and bolts, and gears doing that thing it does. But what is the likelihood of ever getting a structure for my favorite proteins?" The likelihood has been practically 0 for a long time, especially if you're not working with a model organism. It wasn't really an option for most people, so one just needed to think about other tools, other aspects of biology, other experiments, other mechanisms, other models, and so on.
...but then predicting the 3D structure of proteins leveled up with deep learning, from programs like AlphaFold. Now it seems there is a whole new world of structure-function questions and applications for any regular, middle-of-the-road, non-structural biologist. It feels like the deep sequencing revolution from 10-15 years ago. There is more and more attention to the predicted structures from computational biologists looking to make programs that do even better, and from molecular and cellular and developmental biologists who can make use of these predictions. These programs are going through all the protein sequence databases, predicting what-appear-to-be accurate or accurate-enough structures for thousands or hundreds of thousands of proteins. It's reminiscent of the open fire-hydrant-like deluge of sequencing data that began pouring out with Solexa/Illumina technology. It seems a clubhouse I was never cool enough to be allowed in, nor were you, has suddenly opened its doors for everyone...
So... I decided to walk in and have a peep around.
This is what I've found so far.
Pretending to know Predicting a protein structure:
First of all, if you're working with a model organism, your protein-of-interest may already have an AlphaFold structure here: https://alphafold.ebi.ac.uk/ . These structures are already hyperlinked across the internet ; featured in common databases like UniProt. For example, UniProt features both the experimentally-derived and AlphaFold-predicted structures of the human MCM2 protein: https://www.uniprot.org/uniprot/P49736#structure .
If you are working with a non-model organism, or want to predict the 'de novo' structure of a mutated form of a protein, then you can use AlphaFold or other programs yourself. I'll be honest -- it feels like I'm "supposed to be using AlphaFold", but I haven't been. I found two options when setting out to do this:
- AlphaFold
- Robetta (roseTTAFold and other programs)
I just found Robetta so easy to use that I've spent most of my time there: go ahead, sign up, copy/paste a protein sequence, and press go. That's all there is to it.
Things to do with the PDB structure files:
Search structure databases for similar protein structures.
My aim was to use the predicted structures to look for ‘structural homology’ in PDB, AF, and other databases for proteins that are lowly conserved at the sequence level. Ideally, one would just be able to use a "structure BLAST" interface at NCBI. I did not find that, but I found three programs to do structural database searches. Here I will use Drosophila MCM2 from AlphaFold as an example. In some I use a Robetta model for MCM2. At the moment, I have reviewed FoldSeek, DALI, FATCAT, and 3D-surfer. Overall, I am bullish on FoldSeek, DALI, andFATCAT; but I am scratching my head a little bit at 3D-surfer.
FoldSeek:
I’ve found that FoldSeek is fast (in "local mode" : 3Di/AA), and seems to be quite good at known true positive PDB files I give it (e.g. Human or Drosophila protein structures); in my experience, the top hit was exactly the protein used, and all other top hits were actual homologs in other species. I tried to run "TM-align" (global) mode, but tens of minutes later it was still not done and, after being spoiled on the seconds time-scale for "local mode", I threw a tantrum and closed out the tab.
DALI:
I’ve also messed around with DALI (distance matrix alignment method): more info here and here; all refs here.
The DALI server was overloaded, and my jobs were queued. It took a day to get the results back for the structural search of a known protein against PDB. Nonetheless, the top hit was the expected protein, and other top hits were homologs in other species.
In addition to matches and match stats, the results also offered other "buttons" to click and explore. The one I found most interesting for the moment was the "Pfam" button where, if I'm not mistaken, they shown Pfam domains on your protein that were structural matches (as opposed to normal sequence matching of Pfam domains).
FATCAT:
Length vs Sequence Identity |
3D-Surfer:
3D-Surfer offers database searches as well, but the results on knowns were confusing to me… None of the "hits" it showed were MCM2 -- well at least none that I clicked on. Even when I had them show me the results table for 1000 hits, searching only the AlphaFold database, none of the hits were the AlphaFold MCM2 model I used... So, I can’t vouch for 3D-surfer per se (like I can for FoldSeek and Dali), but 3D-surfer does at least give me hits to consider for all my query structures predicted by Robetta for my proteins-of-interest — whereas FoldSeek found no hits for most. So I don't know what to make of the hits it is giving me in that scenario... but I can see that the protein structures returned do look a bit like the queries when it is simple enough to conclude that "by eye".
Compare protein structures to each other:
In addition to searching databases for 'structure hits', I also want to be able to align different structures together. For example, if there are 2 predicted structure models, I want to align them to see the areas of agreement or disagreement. And I want to be able to align known structures to predicted structures. And so on. There are bound to be many tools that do this type of stuff. I know none of them at the moment, although the programs above likely offer this type of service. For example, I know DALI allows you to do pairwise alignments on all your own stuff, not just databases. And FoldSeek should too... though I might have to download it and do that at the command-line. A colleague uses PyMol. For the moment, that's all I have.
RSCB PDB 3D-View and Pairwise Structure Alignment:
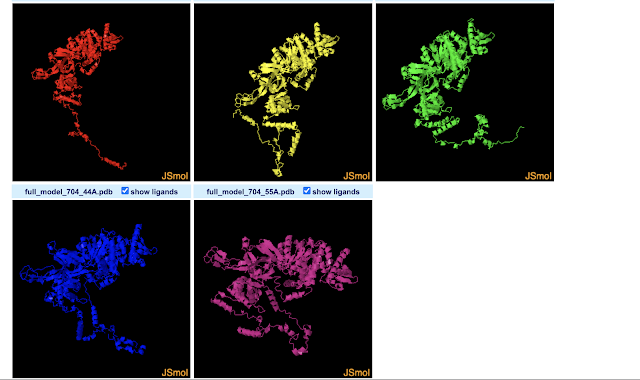
The 3D-View Tool allows you to import multiple PDBs. By default the structures are drawn in different parts of the 3D space. This allows you to compare them by eye, but they are not structurally aligned. While there seem to be buttons concerning aligning the structures, I couldn't figure out how to do that. Meanwhile, the Pairwise Structure Alignment Tool does do structural alignments, allowing a few different ways to do that. I gave all of them a try using the first two models predicted for Drosophila MCM2 by Robetta (which seems to predict 5 by default). Next I will name the alignment modes, and describe how I interpret the results for these two structures based on a nearly absent (but not absent) understanding of what each mode is doing. For more info on what the modes do, see here.
Overall, it appears from a visual point-of-view that the alignment modes fall into roughly 3 categories.
Category 1 : Rigid Optimization
Most modes (4 of 6) fit into what I'd term a "rigid optimization" category: jFATCAT (rigid), jCE, TM-Align, and Smith-Waterman 3D. The all give similar alignments (the SW-3D mode to a lesser extendt). They seem to optimize the amount of the two MCM structure models matching in 3D-space, but do not make changes (or at least not large changes) to the structure or assume it can take on other conformations. The result is that the MCM2 models almost fully align in the ball-of-yarn globular domain(s) of the protein but the N-terminal disordered arms (on bottom left of image) go off in different directions (and are not force aligned in 3D-space). Smith-Waterman 3D, by the looks of it, does the least amount of structure-changing/conforming (or none at all): so while you can see similar structures between models nearby in 3D space, they are much less overlapping than the other 3 modes. Note that FATCAT stands for "Flexible structure AlignmenT by Chaining Aligned fragment pairs allowing Twists". CE stands for "Combinatorial Extension".
- jFATCAT (Rigid) : Gives similar results to jCE and TM-align, and to a lesser-extent, Smith-Waterman 3D. This mode is explained by RCSB as allowing "for flexible protein structure comparison", and, "The rigid flavor of the algorithm is used to run a rigid-body superposition that only considers alignments with matching sequence order. For most structures the performance of this structure alignment is similar to that of CE." Also see: https://fatcat.godziklab.org/fatcat/fatcat_pair.html
- jCE : Gives similar results to jFATCAT (rigid) and TM-align, and to a lesser-extent, Smith-Waterman 3D. RSCB says it "works by identifying segments of the two structures with similar local structure, and then combining those regions to align the maximum number of residues in order to keep the root mean squared deviations (rmsd) between the pair of structures low. This Java port of the original CE uses a rigid-body alignment algorithm. Relative orientations of atoms in the structures being compared are kept fixed during superposition. It assumes that aligned residues occur in the same order in both proteins (i.e., the alignment is sequence-order dependent)."
- TM-align : Gives similar results to jFATCAT (rigid) and jCE, and to a lesser-extent, Smith-Waterman 3D. RCSB explains TM-align as, "Sequence-independent protein structure comparison" that is "sensitive to global topology". Note that TM-align can also be performed at this website that explains TM-Align as "an algorithm for sequence-independent protein structure comparisons. For two protein structures of unknown equivalence, TM-align first generates optimized residue-to-residue alignment based on structural similarity using heuristic dynamic programming iterations."
- Smith-Waterman 3D : Similar to above 3, but more separation between clearly-matching structures. RSCB explains that it "aligns similar sequence segments using Blosum65 scoring matrix ... and aligns two structures based on the sequence alignment." They give the following advice/warnings: "Note that this method works well for structures with significant sequence similarity and is faster than the structure-based methods. However, any errors in locating gaps, or a small number of badly aligned residues can lead to high RMSD in the resulting superposition."
Category 2 : Flexible Optimization
- jFATCAT (flexible) : This seems to further optimize the amount of the two MCM models that match in 3D space by assuming more flexibility/conformational freedom. The net result is basically that it is able to align those disordered N-terminal arms as well. This may be reasonable and the two models may simply reflect that the N-terminal arm is flexible and may take on 1 of multiple conformations. RSCB explains the flexible option in the following way: "The flexible flavor of FATCAT introduces twists (hinges) between different parts of the superposed proteins so that these parts are aligned independently. This makes it possible to effectively compare protein structures that undergo conformational changes in specific parts of the molecule such that global (rigid body) superposition cannot capture the underlying similarity between domains. For example, when the two polymers being compared are in different functional forms (e.g., bound to partner proteins/ligands), were crystallized under different conditions, or have mutations. The downside of this approach is that it can lead to false positive matches in unrelated structures, requiring that results be carefully reviewed." The take-home is that it increases sensitivity at the cost of losing specificity. Also see: https://fatcat.godziklab.org/fatcat/fatcat_pair.html
- jCE-CP : I'm actually not entirely sure how to make sense out of what happened here.... more colors than I expected for one.... RSCB explains it: "Some protein pairs are related by a circular permutation, i.e., the N-terminal part of one protein is related to the C-terminal part of the other or vice versa, or the topology of loops connecting secondary structural elements in a domain are different. Combinatorial Extension with Circular Permutations allows the structural comparison of such circularly permuted proteins." The take-home for this analysis though is that it does not appear to be an appropriate choice.
Evaluating protein structures.
AlphaFold and Robetta may offer scores regarding how confident they are in the protein structures they predict. For example, Robetta offers a confidence score between 0-1. However, one may also be interested in third party programs to run evaluations of experimental- and predicted- structures from various programs. A colleague told me to try "SAVES":
- https://www.doe-mbi.ucla.edu/saves/
- https://saves.mbi.ucla.edu/
It offers a few programs, all you need is the PDB file. Here, again, I will use Drosophila MCM2 from AlphaFold:
- ERRAT: statistics of non-bonded interactions between different atom types ; compares with statistics from highly refined structures.
- Verify3D: Determines the compatibility of an atomic model (3D) with its own amino acid sequence (1D); compares the results to good structures.
- PROVE: Calculates the volumes of atoms in macromolecules; calculates a statistical Z-score deviation for the model from highly refined structures.
- WHATCHECK: extensive checking of stereochemical parameters of the residues in the model.
- PROCHECK: stereochemical quality of residue-by-residue geometry and overall structure geometry.
- CRYST: searches the Protein Data Bank for entries that have a unit cell similar to your input file.